Zad. 1. W pewnej bursie stołowało się czternastu studentów matematyki. Obiady były smaczne, więc cała ekipa zasiadała przy podłużnym stole zawsze w niezmienionym składzie. Każdy miał swoje miejsce wyznaczone według starszeństwa, którego nie wolno było zmieniać. Najmłodszy siadał na szarym końcu, a że półmiski obiegały stół zawsze w tej samej kolejności, zaczynając od najstarszego studenta, dostawały mu się zazwyczaj żałosne resztki potraw. Pewnego dnia zaproponował, aby stołownicy codziennie siadali przy stole w innym porządku aż się wyczerpią wszystkie możliwe kombinacje. Starsi koledzy parsknęli śmiechem. Jak długo studenci musieliby wspólnie jadać obiady, zanim trzeba by jakąś kombinację powtórzyć? Gdyby zaczęli 1 stycznia 2016, to kiedy by skończyli?
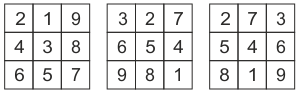
Zad. 2. W kwadracie 3×3 rozmieszczono cyfry od 1 do 9 w taki sposób, że drugi wiersz jest dwukrotnością, a trzeci - trzykrotnością pierwszego. Znajdź to rozmieszczenie.
Zad. 3. Wpisując do kalkulatora graficznego lub programu komputerowego rysującego wykresy funkcji zadanych parametrycznie układ równań:
X = sint, Y = cost (dla 0 < t < 2π oraz -1 < X, Y < 1),
jako wykres otrzymamy okrąg o środku w początku układu współrzednych i promieniu 1,
bo X2 + Y2 = sin2t + cos2t = 1, a to jest właśnie kartezjańskie równanie jednostkowego okręgu. Z którego punktu zaczyna być rysowany ten okrąg? W którą stronę (zegarowo czy antyzegarowo)? Jak zmienić równanie parametryczne, aby okrąg zaczął być rysowany z punktu antypodycznego i w przeciwnym kierunku?
Zadania lutowe okazały się dość trudne. Rzeczywiście przeprowadzenie rachunków w zadaniu 1 bez pomocy kalkulatora Wolframa było dość karkołomne. Za odpowiedź 14! dni przyznawaliśmy 1/4 pkt, gdyż nie wymagała ona użycia kalkulatora ani komputera, a za podanie dokładnej liczby dni lub lat przyznawaliśmy 1/2 pkt, gdyż nie tego dotyczyło pytanie.
Zawodnicy zdobyli następujące liczby punktów:
- 3 - Marzena Wąsiewicz (informatyk, a obecnie gospodyni domowa z Kajetan),
- 2,75 - Wojciech Tomiczek (inżynier z Lipowej),
- 2,5 - Krystyna Lisiowska (redaktor z Warszawy), Piotr Wróbel (inżynier sprzedaży z Brwinowa),
- 2 - Andrzej Piasecki (administrator IT z Oleśnicy), Janusz Szopka,
- 1,5 - Daria Bumażnik (LO 2 Jelenia Góra),
- 1 - Dominik Zygmunt (student bankowości i finansów cyfrowych na UŁ).
Po pięciu miesiącach trwania Ligi prowadzą:
- Marzena Wąsiewicz (14,75 pkt)
- Wojciech Tomiczek (14 pkt)
- Piotr Wróbel (13,75 pkt)
- Andrzej Piasecki (13,25 pkt)
Gratulujemy!
Zad. 1. Wspólne obiadowanie zajęłoby 14! = 87 178 291 200 dni, czyli ponad 230 milionów lat. Jeśli miejsce przy stole byłoby dziedziczone, albo biesiadowanie kontynuowano by w lepszym świecie, to zakończyłoby się (wg. WolframAplha) w czwartek 1 maja 238 688 070 roku (wystarczy wpisać January 1, 2016 + 14! days). Zadanie pochodzi z książki Juliana Tuwima "Cicer cum caule, czyli groch z kapustą" jednak podana tam odpowiedź (14! dni = 238 844 633 lata 4 miesiące i 24 dni) nie jest poprawna, gdyż nie uwzględnia lat przestępnych. Tuwim pomylił się w rachunkach o prawie 160 tysięcy lat. I nie tłumaczy go fakt, że nie było wtedy kalkulatorów, gdyż błąd nie był rachunkowy, tylko koncepcyjny. Aby zobaczyć, jak poradzić sobie z rachunkami bez pomocy Wolphrama Alfa, zrób zadanie 3 z maja 2016.
Zad. 2. Są 4 możliwe rozwiązania.
Zad. 3. Okrąg zaczyna być rysowany z punktu (0, 1), bo dla t=0, mamy X=0 i Y=1. Jest rysowany w kierunku zegarowym, bo dla t>0 współrzędne X są dodatnie. Aby okrąg był rysowany, zaczynając z punktu (0, -1) w kierunku antyzegarowym, równanie parametryczne może być np. takie: X = sint, Y = - cost. Jest to nadal równanie okręgu o środku (0, 0) i promieniu 1, bo X2 + Y2 = sin2t + (-cost)2 = 1. Dla t=0, mamy X=0 i Y=-1, czyli start jest w punkcie (0, -1). Natomiast dla t>0 współrzędne X są dodatnie, wiec rysowanie odbywa się rzeczywiście w kierunku antyzegarowym.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
