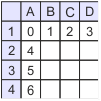
Zad. 1. Jakie liczby wyliczy komputer, jeśli w polu B2 poniższego arkusza kalkulacyjnego wpisano podaną formułę i skopiowano ją do pozostałych pustych komórek? Na czym polega różnica?
a) := A2 – B1
b) :=
c) :=
Zad. 2. Gra "Szachownica" polega na zamienieniu tradycyjnej czarno-białej szachownicy na jednolicie czarną przez inwersję kolorów wszystkich pól wskazanego wiersza lub kolumny na przeciwne. Podaj algorytm, który dla szachownicy o rozmiarach 2n×2n, gdzie n jest liczbą naturalną, pozwala na ukończenie gry w 2n ruchach, np. dla szachownicy 2x2 wystarczą 2 ruchy polegające na inwersji kolorów w I kolumnie i w I wierszu (co zapiszemy jako 1K, 1W).
Zad. 3. Jakie rachunki należy wykonać na kalkulatorze, aby sprawdzić poprawność wyniku zad. 1. luty 2016?
W maju zawodnicy zdobyli następujące liczby punktów:
- 3 - Andrzej Piasecki (administrator IT z Oleśnicy), Marzena Wąsiewicz (informatyk, a obecnie gospodyni domowa z Kajetan)
- 2,5 - Krystyna Lisiowska (redaktor z Warszawy)
- 2 - Daria Bumażnik (uczennica II LO W Jeleniej Górze), Wojciech Tomiczek (inżynier z Lipowej)
- 1,5 - Krzysztof Danielak (student informatyki przemysłowej na PWr), Piotr Wróbel (inżynier sprzedaży z Brwinowa)
- 1 - Dominik Zygmunt (student bankowości i finansów cyfrowych na UŁ).
Po ośmiu miesiącach trwania Ligi prowadzą:
- Marzena Wąsiewicz (23,75 pkt)
- Andrzej Piasecki, Wojciech Tomiczek, Piotr Wróbel (20,75 pkt)
- Krystyna Lisiowska (19,75 pkt)
- Krzysztof Danielak (18,25 pkt)
- Daria Bumażnik (15,5 pkt)
- Dominik Zygmynt (13 pkt)
Gratulujemy!
Zad. 1. Patrząc wierszami, w polach kwadratu B2 - D4 komputer wyliczy:
a) 3 1 -2, 2 1 3, 4 3 0, czyli różnice wartości komórek leżących bezpośrednio po lewej i nad daną komórką
b) 3 2 1, 3 2 1, 3 2 1, czyli różnice wartości komórek A2 i tej z pierwszego wiersza danej kolumny
c) 3 2 1, 4 3 2, 5 4 3, czyli różnice wartości komórek z pierwszej kolumny danego wiersza i z pierwszego wiersza danej kolumny.
Różnice wynikają z zastosowania adresowania względnego (bez dolara) i bezwzględnego (z dolarem). Adresowanie względne wykorzystuje relatywne położenie komórek, dlatego np. formuła "A2-B1" skopiowana z komórki B2 do komórki C2 przybiera postać "B2-C1". W adresowaniu bezwzględnym 
zawsze oznacza komórkę A2, a B€1 oznacza komórkę z kolumny, do której kopiujemy formułę, ale leżącą w pierwszym wierszu.
Zad. 2. Jeden z możliwych algorytmów dokonuje inwersji kolorów najpierw we wszystkich kolumnach o numerach nieparzystych, a potem we wszystkich wierszach o numerach nieparzystych, co daje 2n następujących ruchów: 1K, 3K, 5K, ..., (2n–1)K, 1W, 3W, 5W, ..., (2n–1)W.
Zad. 3. Ponieważ 14! jest podzielne przez 7, wspólne obiadowanie zajmie całkowitą liczbę tygodni. Ponieważ zaczęło się 1 stycznia 2016 roku, który był piątkiem, musi zakończyć się w czwartek. Pozostaje pytanie, jaka będzie wówczas data dzienna. Chcemy ją obliczyć, posługując się konwencjonalnymi operacjami arytmetycznymi i uwzględniając reguły wprowadzania lat przestępnych w kalendarzu gregoriańskim (przestępne są lata o numerach podzielnych przez 4 z wyjątkiem lat sekularnych, czyli zakończonych dwoma zerami, z których przestępne są tylko te o numerach podzielnych przez 400). W kalendarzu juliańskim w ciągu 400 lat wypadało dokładnie 100 lat przestępnych. W kalendarzu gregoriańskim na 400 lat jest ich 97 (3 to lata sekularne niepodzielne przez 400).
Wykonujemy dzielenie całkowite [tex][\frac{14!}{400 \cdot 365 +97}][/tex]= 596 715 reszty 19 845, co oznacza, że obiadowanie zajęło tyle gregoriańskich czterystuleci i 19 845 dni (tj. jeszcze ok. 50 lat), tzn. 400 · 596 715 lat i 19 845 dni, czyli 238 686 000 lat i 19 845 dni.
Wykonujemy dzielenie całkowite [tex][\frac{19845}{4 \cdot 365 +1}][/tex]= 13 reszty 852, co oznacza, że tyle gregoriańskich czteroleci jest w pozostałej liczbie dni i jeszcze 852 dni (tj. ponad 2 lata), tzn. trzeba dodać do 238 686 000 lat jeszcze 4·13 lat i 852 dni, otrzymując 238 686 052 lata i 852 dni.
Ponieważ 852 = 366 + 365 + 121, do wyniku dodajemy jeszcze 2 lata, a początkowe cztery miesiące kolejnego roku dają 31+28+31+30 = 120 dni. Zatem dniem 121. w kolejnym roku jest 1 maja. Uwzględniając, że zanim zaczęliśmy obiadowanie, minęło już 2015 lat naszej ery, trwało ono do roku 2015 + 238 686 052 + 2 = 238688069 i jeszcze 121 dni, czyli zakończyło się 1 maja roku 238688070, co zgadza się z wynikiem otrzymanym za pomocą Wolphrama Alfa z lutego 2016.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
