Zad. 1. W emitowanej ostatnio reklamie telewizyjnej środka na kaszel (Mucosolwan) podano, że płuca człowieka wymieniają 10 tysięcy metrów sześciennych powietrza w ciągu doby. Czy to możliwe? Przedstaw przyjęty model i obliczenia.
Zad. 2. Sześciany pierwszych trzech liczb naturalnych (1, 8 i 27) dają w sumie 36 - liczbę kwadratową. Jakie są trzy następne kolejne liczby naturalne, których suma sześcianów ma tę własność?
Zad. 3. Ile wynosi
.
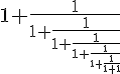Podaj zapis powyższego ułamka w symbolice tex-owej (można skorzystać z samouczka zamieszczonego na stronie głównej w poziomym pasku menu). Ile wynosi wartość analogicznego ułamka o nieskończonej liczbie pięter?
W tym miesiącu następujące liczby punktów zdobyli:
- 3 - Krzysztof Danielak - student informatyki przemysłowej na PWr, Oliwia Makuch - uczennica SP 1 Szprotawa, Andrzej Piasecki - administrator IT z Oleśnicy, Wojciech Tomiczek - inżynier z Lipowej, Marzena Wąsiewicz - informatyk, a obecnie gospodyni domowa z Kajetan, Piotr Wróbel - inżynier sprzedaży z Brwinowa,
- 2,5 - Krystyna Lisiowska - redaktor z Warszawy,
- 2,25 - Dominik Zygmunt - student informatyki przemysłowej na PWr,
- 1,5 - Daria Bumażnik - II LO Jelenie Góra, Kamil Demczyszyn - Lotnicze Zakłady naukowe Wrocław.
Pozostali zawodnicy uzyskali poniżej 1 pkt.
Po dwóch miesiącach trwania Ligi prowadzą:
I m. - Krzysztof Danielak, Andrzej Piasecki, Marzena Wąsiesicz, Piotr Wróbel (6 pkt)
II m. - Wojciech Tomiczek (5,5 pkt)
III m. - Dominik Zygmunt (4,25 pkt)
Gratulujemy!
Zad. 1. Jeden wdech wprowadza do płuc ok. 0,5 dm3 powietrza. Liczba wdechów na minutę to ok. 20. W ciągu minuty wydychamy więc 20·0,0005 m3 = 0,01 m³ powietrza. W ciągu doby wydychamy 24·60·0,01 = 14,4m³ powietrza. W ciągu roku daje to 365·14,4 = 5256 m³. Zatem ilość powietrza podaną w reklamie wydychamy w ciągu prawie dwóch lat, a dokładniej 694 dni i tylukrotny błąd w rachunkach popełnili twórcy reklamy. Prawdopodobnie pomylili po prostu jednostki. Gdyby zamiast m3 podali tę samą wielkość w litrach (czyli dm3), wynik byłby zupełnie realny. A tak pozostał wstyd, chociaż reklamę wycofano z emisji po kilku dniach.
Zad. 2. Szukane liczby to 23, 24 i 25, bo 233+243+253 = 12167+13824+15625 = 41616 = 2042.
Zad. 3. Wartość ułamka wynosi 21/13 ≈ 1,615. Zapis texowy podanego ułamka to:
1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+1}}}}},
przy czym należy go ująć z obu stron w symbole 'dolarów' albo poprzedzić znacznikiem 'tex', a zakończyć '/tex' oba w nawiasach kwadratowych.
W granicy, gdy liczba pięter ułamka rośnie do nieskończoności, otrzymujemy liczbę złotą, która ma najpiękniejsze rozwinięcie w ułamek łańcuchowy 1,(1) - jeden i jeden w okresie. Wartość tę można łatwo obliczyć, zauważając samopodobieństwo nieskończonego ułamka łańcuchowego.
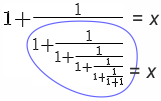
Widzimy, że wielkość ta spełnia równania 1 + 1/x = x, lub równoważnie x2 – x – 1 = 0, którego dodatnim pierwiastkiem jest [tex]\frac{1+\sqrt5}{2}[/tex] ≈ 1,618033988, czyli właśnie liczba złota.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
