grudzień 2015

grudzień 2015

Data ostatniej modyfikacji:
2016-03-26

Zad. 1. Robot DEJ-NO-MI-2 otrzymał następujące polecenie: PODAJ MI SZKLANKĘ LUB KUBEK ORAZ FILIŻANKĘ. Na ile sposobów można to polecenie zinterpretować? Ile rzeczy może podać robot, wykonując to polecenie?

Zad. 2. Jakie zakresy na osiach układu współrzednych należy ustawić na ekranie komputera, aby zaobserwować na nim każdy z punktów przecięcia wykresów funkcji y=x¹⁰ oraz y=2^x? Podaj współrzedne tych punktów z dokładnością do dwóch cyfr znaczących.

Zad. 3. Czy istnieje liczba kwadratowa złożona z cyfr od 1 do 9, w ktorej każda cyfra występuje raz? Jeśli tak, podaj największą i najmniejszą z nich.

Wyniki:

W tym miesiącu nikt nie uzyskał 3 pkt. Natomiast następujące osoby zdobyły takie liczby punktów:

2,75 - Wojciech Tomiczek (inżynier z Lipowej) i Marzena Wąsiewicz (informatyk, a obecnie gospodyni domowa z Kajetan)
2,25 - Andrzej Piasecki (administrator IT z Oleśnicy) i Piotr Wróbel (inżynier sprzedaży z Brwinowa)
1,75 - Krzysztof Danielak (student informatyki przemysłowej na PWr) i Krystyna Lisiowska (redaktor z Warszawy)
1,25 - Kamil Demczyszyn (Lotnicze Zakłady Naukowe Wrocław), Janusz Szopka i
Dominik Zygmunt (student bankowości i finansów cyfrowych na UŁ).

Pozostali zawodnicy otrzymali 1 punkt lub mniej.

Po trzech miesiącach trwania ligi prowadzą:

Marzena Wąsiewicz (8,75 pkt)
Andrzej Piasecki, Wojciech Tomiczek i Piotr Wróbel (8,25 pkt)
Krzysztof Danielak (7,75 pkt).

Gratulujemy!

Odpowiedzi:

Zad. 1. Polecenie nie jest jednoznaczne. Zależy od "rozstawienia nawiasów". Można je zinterpretować na 2 sposoby:

1) Podaj mi (szklankę lub kubek) oraz filiżankę.
Jeśli będzie poprawnie wykonane, robot może podać 2 lub 3 rzeczy.

2) Podaj mi szklankę lub (kubek oraz filiżankę).
Jeśli będzie poprawnie wykonane, robot może podać 1, 2 lub 3 rzeczy.

Zad. 2. Są trzy(!) punkty przecięcia podanych wykresów. Ich współrzędne x wynoszą: dla pierwszego punktu około -1, dla drugiego - około 2, a dla trzeciego - między 50 a 60.

Dwa pierwsze punkty można łatwo zobaczyć jednocześnie na ekranie, np. na zakresie osi x [-2, 2] i osi y [0, 3]. Przybliżone do dwóch cyfr znaczących współrzędne tych punktów przecięcia to (-0,9; 0,5) i (1,1; 2,1).

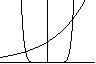
Trzeci punkt przecięcia nie da się zaobserwować jednocześnie z poprzednimi, ale ponieważ funkcja wykładnicza dla dużych argumentów rośnie szybciej niż jakakolwiek funkcja wielomianowa, wiadomo, że kiedyś wykres 2^xprzeskoczy powyżej wykresu x¹⁰. Przybliżoną wartość x tego punktu można łatwo oszacować.

x > 10, bo 10¹⁰ > 2¹⁰ = 1024 ≈ 10³
x > 30, bo 30¹⁰ > 2³⁰= (2³)¹⁰ = 8¹⁰
x > 50, bo 50¹⁰ > 2⁵⁰ = (2⁵)¹⁰ = 32¹⁰
x < 60, bo 60¹⁰ < 2⁶⁰ = (2⁶)¹⁰ = 64¹⁰.

Skoro współrzędna x trzeciego punktu przecięcia leży między 50 a 60, to jego współrzędna y leży między 2⁵⁰ ≈ 10¹⁵ a 2⁶⁰ ≈ 10¹⁸. Przy takim zakresie na osi y nie można zobaczyć punktów o wartościach między 0 a 2. Trzeci punkt przecięcia trzeba oglądać osobno. Odpowiedź, że zakres osi x wynosi [-1, 60], a osi y [0, 10¹⁸] nie mogła więc być uznana za poprawną. Aby zaobserwować trzeci punkt przecięcia, zakresy na osiach mogą być np. takie: oś x [55, 60], oś y [10^17, 10^18], a współrzędne szukanego punktu, to w przybliżeniu (58; 4,3*10^17).