Zad. 1. W trójkącie ABC środkowe AL i BM przecinają się w punkcie K. Wierzchołek C leży na okręgu przechodzącym przez K, L i M. Oblicz długość środkowej CN, wiedząc, że |AB| = a.
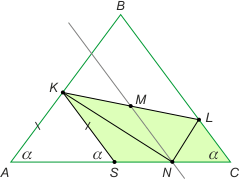
Zad. 2. W trójkącie równoramiennym na ramionach AB i BC obrano odpowiednio punkty K i L takie, że |AK| + |CL| = |KL|. Przez środek M odcinka KL poprowadzono prostą równoległą do boku BC przecinającą bok AC w punkcie N. Znajdź miarę kąta KNL.
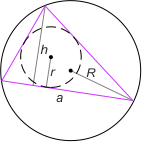
Zad. 3. Wykaż, że w trójkącie zachodzi nierówność: R/r > a/h, gdzie R jest promieniem okręgu opisanego na tym trójkącie, r - promieniem okręgu wpisanego w trójkąt, a - najdłuższym bokiem, a h - najkrótszą wysokością.
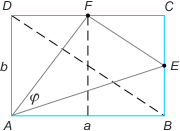
Zad. 4. (wolna amerykanka) Stosunek pola prostokąta ABCD do kwadratu długości jego przekątnej wynosi k. Oblicz miarę kąta EAF, gdzie punkty E i F są odpowiednio środkami boków BC i CD.
Maksymalną liczbę 30 punktów za zadania 1-3 otrzymują: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Iwona Gruszecka (nauczycielka, G 42 Warszawa), Mateusz Klein (uczeń, III LO Gdynia), Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas (student, PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Sabina Khady Sy (studentka, UJ), Mikołaj Szamajew (uczeń, Szkoła Ogólnokształcąca nr 131 Charków, Ukraina), Feliks Pobiedziński (uczeń, I LO Kraków), Sławomir Matysiak (nauczyciel, PZS 1 Trzebnica). 28 punktów uzyskał Jakub Gajdecki (uczeń, VIII LO Katowice).
Zadanie 4 w pełni poprawnie rozwiązali i uzyskali 10 punktów: Jacek Bagiński, Włodzimierz Bąk, Jakub Gajdecki, Mateusz Klein, Zygmunt Krawczyk, Michel Migas, Tadeusz Porzucek, Sabina Khady Sy, Mikołaj Szamajew, Wojciech Tomiczek (inżynier, Lipowa).
Gratulacje!
Zad. 1. Zauważmy, że odcinek ML jest równoległy do boku AB i dwa razy od niego krótszy. Środkowa CN dzieli go na połowy. Punkt K jest środkiem ciężkości trójkąta i dzieli środkową CN na odcinki KN i KC o długościach |KN| = x/3 oraz |KC| = 2x/3 = x/2 + x/6. Z twierdzenia o przecinających się cięciwach okręgu otrzymujemy równanie a/4·a/4 = x/2·x/6, skąd x = a√3/2.
Zad. 2. Obierzmy na boku AC punkt S tak, że odcinek KS jest równoległy do BC. Wówczas |KS| = |AK|. Rozważmy teraz trapez KSLC. Odcinek MN jest linią średnią, wobec tego |MN| = 1/2 (|KS|+|LC|) = 1/2 (|AK|+|LC|) = 1/2 |KL|. Zatem |MK| = |ML| = |MN|. Oznacza to, że punkty
K, L i N leżą na okręgu o środku M i kąt KNL jest prosty.
Zad. 3. Zachodzi 2r < h, bo okrąg wpisany zawiera się we wnętrzu trójkąta. Niech B, C to końce najdłuższego boku, a O – środek okręgu opisanego na trójkącie. Z nierówności trójkąta dla ΔBOC zachodzi 2R>a. Wobec tego R/r > R/h/2 = 2R/h > a/h.
Zad. 4. Z założenia otrzymujemy k = ab/a2+b2. Zauważmy, że tgφ = tg(∡FAB–∡EAB) = (2b/a–b/2a)/(1+2b/a·b/2a) = 3b/2a : (a2+b2)/a2 = 3/2 · ab/a2+b2 = 3k/2. Stąd φ = arctg 3k/2.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
