Zad. 1. W równoległoboku ABCD punkt E jest środkiem boku AD. Niech F będzie rzutem prostopadłym wierzchołka B na prostą CE. Wykaż, że trójkąt ABF jest równoramienny.
Zad. 2. W trójkącie ABC poprowadzono dwusieczne AD i BE. Wiedząc, że DE jest dwusieczną kąta ADC, oblicz miarę kąta A.
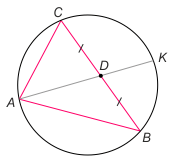
Zad. 3. Środkową AD trójkąta ABC przedłużono do przecięcia się w punkcie K z okręgiem opisanym na tym trójkącie. Wykaż, że długość odcinka BD jest średnią geometryczną długości odcinków AD i DK.
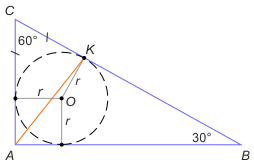
Zad. 4. (wolna amerykanka) W trójkącie prostokątnym jeden z kątów ostrych ma miarę 30°. W trójkąt wpisano okrąg o promieniu r. Oblicz odległość wierzchołka kąta prostego od punktu styczności leżącego na przeciwprostokątnej.
Maksymalną liczbę 30 punktów za zadania 1-3 otrzymali: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Jakub Gajdecki (uczeń, VIII LO Katowice), Iwona Gruszecka (nauczycielka, G 42 Warszawa), Mateusz Klein (uczeń, III LO Gdynia), Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas (student, PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Sabina Sy (studentka, UJ), Mikołaj Szamajew (uczeń, Szkoła Ogólnokształcąca nr 131 Charków, Ukraina), Feliks Pobiedziński (uczeń, I LO Kraków), Sławomir Matysiak (nauczyciel, ZS1 Trzebnica), Anna Pawlus (uczennica, VIII LO Katowice).
Za zadanie 4 10 punktów otrzymali: Jacek Bagiński, Włodzimierz Bąk, Jakub Gajdecki, Mateusz Klein, Zygmunt Krawczyk, Michel Migas, Tadeusz Porzucek, Sabina Sy, Mikołaj Szamajew, Feliks Pobiedziński oraz Wojciech Tomiczek (inżynier, Lipowa).
Gratulacje!
Aktualna czołówka Ligi Geometrycznej:
- Włodzimierz Bąk, Iwona Gruszecka, Mateusz Klein, Michel Migas oraz Tadeusz Porzucek (120 pkt)
- Zygmunt Krawczyk (112 pkt).
Czołówka w kategorii "wolna amerykanka":
- Jacek Bagiński, Włodzimierz Bąk, Jakub Gajdecki, Mateusz Klein, Zygmunt Krawczyk, Michel Migas, Sabina Sy, Wojciech Tomiczek (40 pkt.)
- Tadeusz Porzucek (38 pkt.).
Zad. 1. Niech K będzie punktem wspólnym prostych CE i AB. Trójkąty KAE i ECD są przystające (kbk), zatem punkt A jest środkiem odcinka KB, a odcinek FA jest środkową trójkąta prostokątnego KBF opuszczoną z wierzchołka kąta prostego. Wynika stąd, że FA jest połową przeciwprostokątnej KB (warunek opisania okręgu na trójkącie prostokątnym), więc |AF| = |AB|.
Zad. 2. Zauważmy, że punkt E jest środkiem okręgu dopisanego do trójkąta ABD, stycznego do boku AD (bo leży na przecięciu dwusiecznych kąta wewnętrznego i zewnętrznego trójkąta). Zatem AC zawiera się w dwusiecznej kąta zewnętrznego DAX. Oznacza to, że 3α = 180°. Zatem |∡BAC| = 120°.
Zad. 3. Z twierdzenia o przecinających się cięciwach okręgu mamy |AD|·|DK| = |BD|·|DC|, a wobec |BD| = |DC| mamy tezę.
Zad. 4. Odcinki CK i KO są bokami trójkąta ekierkowego COK (kąty 30°, 60°, 90°). Stąd CK = r√3. Z twierdzenia kosinusów w trójkącie AKC mamy
|AK|2 = (r√3+r)2 + (r√3)2 – 2r√3·(r√3+r)·cos60°, skąd |AK| = r√(4 + √3).
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
