Zad. 1. Papierowy trójkąt prostokątny zginamy wzdłuż boku tak, by wierzchołek kąta prostego pokrył się z drugim wierzchołkiem. W jakim stosunku przecinają się przekątne powstałego czworokąta?
Zad. 2. Okręgi dopisane do trójkąta ABC są styczne do boków AC i BC odpowiednio w punktach K i L. Wykaż, że prosta przechodząca przez środki odcinków KL i AB dzieli obwód trójkąta na pół. (Okrąg dopisany jest styczny do jednego z boków trójkąta i przedłużeń pozostałych boków.)
Zad. 3. Niech AH będzie wysokością w trójkącie ABC, a M i N rzutami spodka tej wysokości odpowiednio na boki AC i AB. Wykaż, że jeśli środek okręgu opisanego na trójkącie leży na odcinku MN, to odcinek ten dzieli pole trójkąta na połowy.
Zad. 4. (wolna amerykanka) W trójkącie prostokątnym ABC środek okręgu weń wpisanego dzieli dwusieczną BE kąta prostego w stosunku √3:√2, licząc od wierzchołka B. Znajdź miary kątów ostrych tego trójkąta.
Za zadania 1-3 maksymalną liczbę 30 punktów otrzymali: Włodzimierz Bąk (nauczyciel I LO Opole), Iwona Gruszecka (nauczycielka GM 42 Warszawa), Mateusz Klein (uczeń III LO Gdynia), Michel Migas (student PW), Wioleta Pilzak (studentka PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń). 28 punktów zdobył Mikołaj Szamajew (uczeń, Szkoła Ogólnokształcąca nr 131 Charków, Ukraina), 22 punkty - Zygmunt Krawczyk (nauczyciel SLO Żary), 20 punktów - Jacek Bagiński (nauczyciel I LO Kraków)
Za zadanie 4 (wolna amerykanka) 10 punktów uzyskali: Jacek Bagiński, Włodzimierz Bąk, Jakub Gajdecki (uczeń VIII LO Katowice), Zygmunt Krawczyk, Mateusz Klein, Michel Migas, Wioleta Pilzak, Sabina Sy (studentka UJ), Wojciech Tomiczek (inżynier, Lipowa), a 8 punktów zdobył Tadeusz Porzucek i Mikołaj Szamajew.
Gratulacje.
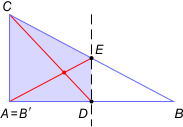
Zad. 1. Trójkąt ABC zaginamy wzdłuż prostej DE prostopadłej do AB, tak aby wierzchołek B pokrył się z A. Zauważmy, że przekątne czworokąta ADEC są jednocześnie środkowymi trójkąta ABC, więc przecinają się w stosunku 2:1.
Zad. 2. Suma długości odcinków AY i AK' jest równa obwodowi trójkąta ABC. Mamy zatem |AK'| = |AY| = p, gdzie p oznacza połowę obwodu trójkąta. Analogicznie |BX| = |BL'| = p. Zatem |AL| = |BK| = p–|AB|. Ponieważ trapez ABB'A' jest równoramienny, kąty LAA' i KBB' są przystające. Oznacza to, że odcinki KK' i LL' są równoodległe od odcinków BB' i AA'. Stąd linia średnia MM' trapezu ABB'A' jest jednocześnie linią średnią trapezu LKK'L' i dzieli przekątną AB' na połowy. Ponieważ |AB'| = |AC|+|CB'| = |AC|+|CB|, otrzymujemy tezę.
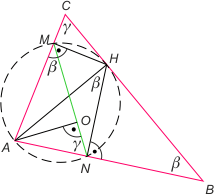
Zad. 3. Zauważmy, że na czworokącie ANHM można opisać okrąg (suma miar przeciwległych kątów ANH i AMH wynosi 180°), którego średnicą jest odcinek AH. Kąt HAN ma miarę 90°–β (jako kąt trójkąta HAB), a stąd kąt AHN ma miarę β. Zatem kąt AMN również ma miarę β (wpisany oparty na tym samym łuku). Z tego wynika, że kąt MNA ma miarę γ, a trójkąty ABC i AMN są podobne (kąt α mają wspólny).
Niech O będzie środkiem okręgu opisanego na trójkącie ABC. Zauważmy, że AO jest wysokością trójkąta AMN, bowiem |∡ONA| = |∡MNA| = γ oraz |∡OAN| = 90–γ, jako kąt przy podstawie trójkąta równoramiennego AOB (|OA|=|OB|=R), w którym |∡AOB| = 2γ (kąt środkowy oparty na tym samym łuku, co kąt wpisany ACB).
Wiadomo, że stosunek pól figur podobnych jest kwadratem skali podobieństwa. Skalę podobieństwa trójkątów ABC i AMN możemy wyznaczyć na dwa sposoby: jako stosunek wysokości opuszczonych z wierzchołka A lub jako stosunek średnic okręgów opisanych. Otrzymujemy z jednej strony PAMN/PABC = (OA/AH)2 = R2/(AH)2, a z drugiej PAMN/PABC = (AH)2/4R2. Mnożąc stronami te równości, otrzymujemy (PAMN/PABC)2 = 1/4. Stąd PAMN/PABC= 1/2.
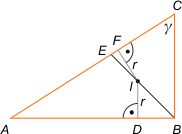
Zad. 4. (wolna amerykanka) Oznaczmy przez I środek okręgu wpisanego w trójkąt i rozważmy trójkąty IDB oraz IEF. W każdym z nich wyliczymy promień r. Z trójkąta IDB mamy r = |ID|·sin45°, a z trójkąta IEF mamy r = |IE|·sin(135°-γ). Otrzymujemy równanie
|IB|/|IE| = sin(135°-γ)/√2/2 = √3/√2, skąd γ = 15° lub γ = 75° i takie właśnie miary mają kąty ostre trójkąta.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
