Zadanie 1. Niech AD będzie średnicą okręgu opisanego na trójkącie ABC. Wykaż, że ortocentrum H (czyli punkt przecięcia prostych zawierających wysokości trójkąta) leży symetrycznie do punktu D względem środka boku BC.
Zadanie 2. Przez dowolny punkt wewnątrz trójkąta ABC prowadzimy proste równoległe do jego boków. Dzielą one trójkąt na sześć figur, z których trzy są trójkątami o polach S1, S2, S3.
Wykaż, że [tex]S_{ABC}\left( \sqrt{S_1}+ \sqrt{S_2}+ \sqrt{S_3} \right)^2[/tex].
Zadanie 3. Z dwóch wierzchołków trójkąta prowadzimy dwusieczne kątów zewnętrznych tak, że obie leżą po jednej stronie boku łączącego te wierzchołki (po tej samej, co trzeci wierzchołek). Trzeci wierzchołek rzutujemy prostopadle na te dwusieczne. Wykaż, że odległość rzutów dla danego trójkąta jest stała, tzn. nie zależy od boku, dla którego przeprowadzimy tę konstrukcję.
Tym razem komplet punktów zdobyli panowie Jacek Bagiński (nauczyciel, I LO Kraków, w sumie 166 pkt w Lidze), Krzysztof Sobków (nauczyciel, II LO Opole, w sumie 160 pkt) oraz Arkadiusz Wróbel (student, Brwinów, 158 pkt). Gratulujemy.
Zadanie 1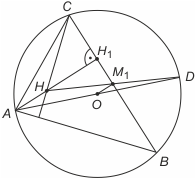
Wystarczy zauważyć, że w trójkącie AHD odcinek OM1 jest równoległy do AH (bo oba leżą na prostych prostopadłych do BC) i jest linią średnią (bo połowi bok AD). Zatem punkt M1 jest środkiem odcinka HD. Stąd mamy tezę.
Zadanie 2
Zauważmy, że trójkąty o polach S1, S2 i S3 są podobne do wyjściowego trójkąta ABC w skalach odpowiednio k1=x/c, k2=y/c i k3=z/c. Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa, skąd otrzymujemy równość √S1/√SABC + √S2/√SABC + √S3/√SABC = x/c + y/c + z/c = c/c = 1. Stąd po przekształceniu mamy tezę.
Zadanie 3
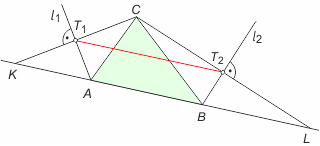Zauważmy, że trójkąty ACT1 i AT1K są przystające z cechy kbk (jednakowe kąty przy wierzchołku A, wspólny bok AT1 i kąt prosty). Wówczas AK = AC. Analogicznie BL = BC. Oznacza to, że odcinek KL ma długość równą obwodowi trójkąta ABC. Zauważmy, że odcinek T1T2 jest linią średnią w trójkącie KLC, stąd jego długość jest równa połowie obwodu wyjściowego trójkąta. Wynik ten nie zależy od wyboru boku, dla którego przeprowadzamy tę konstrukcję (w tym wypadku dla boku AB).
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
