Zadanie 1. Na trójkącie ABC opisano okrąg. Styczna do okręgu w punkcie B przecina prostą AC w punkcie M. Znajdź stosunek długości AM do MC, jeśli stosunek długości AB do BC wynosi k.
Zadanie 2. W trapezie ABCD ramię AD jest prostopadłe do podstaw oraz AD = [tex]\sqrt{AB \cdot DC}[/tex]. Niech E będzie punktem przecięcia przedłużeń ramion trapezu, O punktem przecięcia przekątnych, a M środkiem ramienia AD. Oblicz rozwartość kąta EOM.
Zadanie 3. Dwa okręgi są styczne wewnętrznie w punkcie A. Ze środka O większego okręgu poprowadzono promień OB styczny do mniejszego okręgu w punkcie C. Oblicz rozwartość kąta BAC.
Kwietniową serię zadań poprawnie rozwiązali: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Anna Gudełajtis (uczennica, II LO Opole), Krzysztof Sobków (nauczyciel, II LO Opole), Arkadiusz Wróbel (student, Brwinów), Tadeusz Porzucek (emeryt, Gostyń), Antoni Kamiński (uczeń, IIILO Wrocław). Gratulujemy!

Zadanie 1
Zauważmy, że kąt ABM ma miarę γ, bo jest to kąt dopisany oparty na tym samym łuku, co kąt wpisany ACB. Zatem z cechy k-k trójkąty ABM i i MBC są podobne. Mamy k = AB/BC = AM/BM, skąd BM = AM/k. Z drugiej strony BM/AM = CM/BM. Po podstawieniu za BM otrzymujemy AM/CM = k2.

Zadanie 2
Warunek AD = [tex]\sqrt{AB\cdot DC}[/tex] jest równoważny warunkowi AD2 = AB·DC, czyli AD/AB = DC/AD. Wynika stąd, że trójkąty prostokątne ADC i ABD są podobne, przy czym ∡DAC = ∡ABD = β. Zatem α+β = 90°, czyli ∡AOD = ∡DOC. Można łatwo udowodnić, że w każdym trapezie środki podstaw, punkt przecięcia przekątnych i punkt wspólny przedłużeń ramion są współliniowe (dlaczego?). Korzystając z tego, oraz z faktu, że środkowa przeciwprostokątnej dzieli trójkąt prostokątny na dwa trójkąty równoramienne (dlaczego?), otrzymujemy ∡DOK = β i ∡MOD = α. Stąd ∡EOM = α+β = 90°.
 Zadanie 3
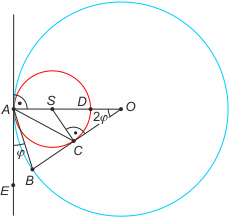
Zadanie 3
Poprowadźmy styczną do obu okręgów w punkcie A. Niech kąt dopisany EAB oparty na łuku AB ma miarę φ. Wówczas kąt środkowy AOB oparty na tym samym łuku ma miarę 2φ. Kąt ASC jest zewnętrzy dla trójkąta COS, więc ma miarę 90°+2φ. Z równoramienności trójkąta ACS kąt SAC ma miarę 45°-φ, a stąd kąt BAC ma miarę 90° - φ - (45°-φ) = 45°.




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
