Zad. 1. W czworokącie ABCD mamy |AB| = |BC| = 1 oraz |∡B| = 100° i |∡D| = 130°. Oblicz długość BD.
Zad. 2. W trójkącie ABC kąty przy wierzchołkach B i C mają po 40°, a BD jest dwusieczną kąta B. Wykaż, że |BD| + |DA| = |BC|.
Zad. 3. W trójkącie ABC poprowadzono wysokość AH i dwusieczną BE. Wiadomo, że |∡BEA| = 45°. Oblicz miarę kąta EHC.
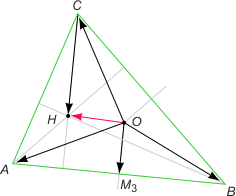
Zad. 4. (wolna amerykanka) Wykaż wzór Hamiltona, tzn. OH = OA + OB + OC (suma wektorów), gdzie O jest środkiem okręgu opisanego na trójkącie ABC, a H - jego ortocentrum, czyli punktem przecięcia wysokości.
Maksymalną liczbę 30 punktów za zadania 1-3 otrzymali: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Mateusz Klein (uczeń, III LO Gdynia), Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas (student, PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń) oraz Sławomir Matysiak (nauczyciel, ZS nr 1 Trzebnica). 20 punktów zdobyła Iwona Gruszecka (nauczyciel, G 42 Warszawa).
W kategorii "wolna amerykanka" 10 punktów zdobyli: Jacek Bagiński, Włodzimierz Bąk, Mateusz Klein, Zygmunt Krawczyk, Michel Migas, Tadeusz Porzucek, Sabina Sy (studentka, UJ) oraz Wojciech Tomiczek (inżynier, Lipowa).
Gratulacje!
Zad. 1. Miary kątów wskazują, że punkty C, D i A leżą na okręgu o środku w B. Stąd |BD| = 1.
Zad. 2. Niech D' leży na BC i |BD'| = |BD|. W trójkącie BD'D mamy kąty 20°, 80°, 80°. Oznacza to, że trójkąt D'CD jest równoramienny i |D'C| = |D'D|, bo kąt zewnętrzny przy wierzchołku D' ma 80° = 40° + 40°. Na czworokącie BD'DA można opisać okrąg, bo suma miar kątów przy D' i A wynosi 180°. Mamy |D'D| = |DA|, bo BD jest dwusieczną kąta B. Stąd |BC| = |BD'|+|D'C| = |BD|+|DA|.
Zad. 3. Niech M będzie rzutem prostokątnym wierzchołka A na dwusieczną BE. Wówczas trójkąt AME jest równoramienny. Zauważmy, że na czworokącie ABHM można opisać okrąg, którego średnicą jest AB. Zatem |AM| = |MH|, bo na tych cięciwach opierają się jednakowe kąty. Otrzymujemy |EM| = |AM| = |MH|, co oznacza, że punkty A, H i E leżą na okręgu o środku w M. Zauważmy, że |∡AHE| = 45°, bo jest on kątem wpisanym opartym na łuku AE i dwa razy mniejszym od kąta środkowego AME, który jest prosty. Stąd szukany kąt EHC ma też 45°.
Zad. 4. Skorzystamy z faktu że |CH| = 2|OM3| udowodnionego w zadaniu 3 z maja 2015. Zauważmy, że OH = OC+CH = OC+2OM3 = OC+OA+AM3+OB+BM3 = OA+OB+OC, bo wektory AM3 i BM3 są przeciwne.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
