Zad. 1. Wykaż, że jeśli stosunek pól dwóch trójkątów prostokątnych równy jest stosunkowi kwadratów długości ich przeciwprostokatnych, to te trójkąty są podobne.
Zad. 2. Dany jest trójkąt prostokątny o przyprostokątnych 3 i 4. Środkowa opuszczona na przeciwprostokątną dzieli go na dwa mniejsze trójkąty. Oblicz odległość środków okręgów wpisanych w te trójkąty.
Zad. 3. Przekątne trapezu mają długości 15 i 20, a linia średnia 12,5. Oblicz wysokość tego trapezu.
Zad. 4. (wolna amerykanka) Wewnątrz kąta prostego znajduje się punkt M odległy od ramion kąta o 3 i 5. Czy da się przez ten punkt poprowadzić prostą, która wraz z ramionami kąta odcina trójkąt o polu 28?
30 pkt. za zadania 1-3 zdobyli: Jacek Bagiński (nauczyciel, I LO Kraków), Włodzimierz Bąk (nauczyciel, I LO Opole), Mateusz Klein (absolwent, III LO Gdynia), Zygmunt Krawczyk (nauczyciel, SLO Żary), Michel Migas (student, PW), Tadeusz Porzucek (emerytowany nauczyciel, Gostyń), Mikołaj Szamajew (uczeń, Szkoła Ogólnokształcąca 131 Charków, Ukraina), Sławomir Matysik (nauczyciel, ZS nr 1 Trzebnica). 18 pkt. zdobyła Iwona Gruszecka (nauczyciel, G 42 Warszawa).
10 pkt. za zadanie 4 zdobyli: Jacek Bagiński, Włodzimierz Bąk, Mateusz Klein, Zygmunt Krawczyk, Michel Migas, Tadeusz Porzucek, Mikołaj Szamajew oraz Sabina Sy (studentka, UJ) i Wojciech Tomiczek (inżynier z Lipowej)
Na zakończenie tegorocznej edycji Ligi Zadaniowej z Geometrii Elementarnej podajemy uczestników, którzy zdobyli ponad 100 pkt. na 270 możliwych za zadania 1-3:
- Włodzimierz Bąk, Michel Migas - 270 pkt.
- Tadeusz Porzucek - 262 pkt.
- Jacek Bagiński - 250 pkt.
- Mateusz Klein - 240 pkt.
- Mikołaj Szamajew - 238 pkt.
- Zygmunt Krawczyk - 230 pkt.
- Iwona Gruszecka - 198 pkt.
- Sławomir Matysiak - 180 pkt.
- Sabina Sy - 108 pkt.
W kategorii "wolna amerykanka" punktacja z całej edycji jest następująca (na możliwe maksimum wynoszące 90 pkt):
- Jacek Bagiński, Włodzimierz Bąk, Zygmunt Krawczyk, Michel Migas, Sabina Sy, Wojciech Tomiczek - 90 pkt.
- Tadeusz Porzucek - 88 pkt.
- Mateusz Klein i Mikołaj Szamajew - 78 pkt.
Serdecznie dziękujemy wszystkim za wzięcie udziału w tegorocznej "zabawie z geometrią". Gratulujemy dobrych rozwiązań i zapraszamy do kolejnej edycji od października.
Życzymy udanych, zdrowych i wartościowych wakacji.
Zad. 1. Niech CD, CE oraz C'D' i C'E' oznaczają wysokości i środkowe opuszczone na przeciwprostokątną odpowiednio w trójkątach ABC i A'B'C'. Z założenia |AB|·|CD|/|A'B'|·|C'D'| = |AB|2/|A'B'|2, skąd mamy |CD|/|C'D'| = |AB|/|A'B'|. Oznacza to, że trójkąty prostokątne CDE i C'D'E' są podobne. Zatem kąty DEC i D'E'C' są przystające. Zauważmy teraz, że trójkąty AEC i CEB są równoramienne. Analogicznie równoramienne są trójkąty A'E'C' oraz C'E'B'. Ponieważ kąty DEC i D'E'C' są zewnętrzne w odpowiednich trójkątach, otrzymujemy przystawanie kątów EBC i E'B'C' (oba są równe połowie kąta DEC). Z drugiej strony mamy równość miar kątów EAC i E'A'C' (90° - |∡DEC|/2). To kończy dowód podobieństwa trójkątów ABC i A'B'C' na mocy cechy kkk.
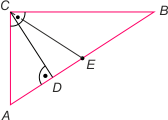
Zad. 2. Zauważmy, że trójkąty AMC i CMB są równoramienne, a dwusieczne kątów przy wierzchołku M są jednocześnie symetralnymi boków AC i BC. Oznacza to, że czworokąt KMLC jest prostokątem. Z twierdzenia o dwusiecznej kąta wewnętrznego dla trójkątów CKM i CML mamy |KS1|/|S1M| = |CK|/|CM| = 3/5 oraz |LS2|/|S2M| = |LC|/|CM| = 4/5, skąd łatwo otrzymujemy |S1M| = 5/4 oraz |S2M| = 5/6. Stosując twierdzenie Pitagorasa do trójkąta S1MS2, otrzymujemy |S1S2| = (5√13)/12.
Zad. 3. Wykorzystamy fakt, że długość linii średniej trapezu jest średnią arytmetyczną długości jego podstaw. Niech CE będzie równoległy do DB. Wówczas |AE| = |AB| + |DC| = 2·12,5 = 25. Wynika stąd, że trójkąt ACE jest prostokątny. Obliczając jego pole dwoma sposobami, otrzymujemy h = 12.
Zad. 4. (wolna amerykanka) Rozwiążmy na początek następujące zadanie: przez punkt M wewnątrz kąta o wierzchołku O należy poprowadzić prostą odcinającą wraz z ramionami kąta trójkąt o najmniejszym polu.
Wykażemy, że szukana prosta przecina ramiona kąta w punktach A i B, takich że |AM| = |MB|. Poprowadźmy przez M inną prostą przecinającą ramiona kąta w punktach X i Y. Przez punkt A poprowadźmy równoległą do ramienia OB. Zauważmy, że trójkąty ACM i XMB są przystające (cecha kbk). Widać, że POAB = POACX < POYX. Drugi rysunek pokazuje, że POAB = 2 POFME = 2|OF|·|OE|·sinφ, gdzie OFME jest równoległobokiem.
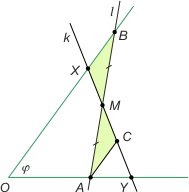
Stosując uzyskany powyżej wynik do wyjściowego zadania, otrzymujemy, że najmniejsze pole wynosi 30, zatem nie można odciąć trójkąta o polu 28.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
