Od stycznia 2014 zadania z Ligi Kalkulatorowo-Komputerowej należy wysyłać na adres mejlowy: mikolaj@math.uni.wroc.pl. Adres pocztowy pozostaje bez zmian.
Zad. 1. Za pomocą kalkulatora prostego znajdź wszystkie liczby, które są:
a) 2003-krotnie b) 2004-krotnie c) 2005-krotnie większe od sumy swoich cyfr.
Ile liczb wystarczy sprawdzić w każdym przypadku?
Zad. 2. Twój domowy robot kuchenny ma do dyspozycji paczkę 100 jednorazowych kubeczków do napojów ustawionych w wieżę denkami do góry. Robot potrafi wykonywać następujące instrukcje: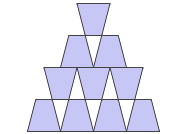
↑ = złap kubek i podnieś w górę
↓ = opuść kubek w dół i puść
→ = przesuń ramię o pół szerokości kubka w prawo
← = przesuń ramię o pół szerokości kubka w lewo
↔ = obróć kubek do góry nogami.
Co powstanie kiedy robot wykona poniższy ciąg instrukcji?
↑ → → ↓ ← ← ↑ → → → → ↓ ← ← ← ← ↑ → → → ↓
Jaki ciąg instrukcji spowoduje, że robot ustawi konstrukcję z rysunku?
Zad. 3. Ekran kalkulatora graficznego lub komputera ustawiono na zakres [0, 10] na obu osiach. Na ekranie wyświetlono odcinek AB o wierzchołkach A(7, 7) i B(8, 7). Niech ekran przedstawia salę gimnastyczną o wysokości 10, a odcinek - zawieszony w niej kosz (widok z boku). Podaj takie wartości a, aby piłka wyrzucana z punktu (0, 0) i lecąca po paraboli y = ax2+bx wpadła do kosza, nie dotykając sufitu, jeśli: a) b=3, b) b=4, c) b=5.
Wydaje się, że zadanie 1 sprawiło zawodnikom nieco kłopotów. Uznawaliśmy w nim oszacowanie liczby sprawdzeń z góry w każdym przypadku nie przekraczające 45. W zadaniu 2 za podanie przykładowych poprawnych wartości a we wszystkich przypadkach przyznawaliśmy 1/2 pkt. W efekcie maksymalną liczbę 3 pkt. uzyskała w tym miesiącu tylko Krystyna Lisiowska - redaktor z Warszawy. Po 2,5 pkt. otrzymali: Daria Bumażnik z II LO w Jeleniej Górze, Andrzej Piasecki - administrator IT z Oleśnicy i Marzena Wąsiewicz - z wykształcenia informatyk, a obecnie gospodyni domowa z Kajetan, 2 pkt. zdobyła Kamila Bojar z ZSP w Szprotawie, 1,5 pkt. - Krzysztof Danielak z I LO w Jeleniej Górze, i 1 pkt. - Piotr Wróbel - inżynier sprzedaży z Brwinowa. Pozostali zawodnicy otrzymali poniżej 1 punktu.
Na półmetku Ligi z Kalkulatorem i Komputerem w czołówce zdecydowaną przewagę ma płeć piękna (wbrew obiegowym opiniom o tym dziale matematyki):
- 14 pkt. - Marzena Wąsiewicz
- 13,5 pkt. - Krystyna Lisiowska
- 13 pkt. - Daria Bumażnik, Andrzej Piasecki.
Zad. 1. Szukane liczby są co najwyżej 5-cyfrowe, bo:
- dla liczb 6-cyfrowych wystarczy rozważyć sumy cyfr od 50 do 54 (tylko one pomnożone przez 2003, 2004 lub 2005 dają wyniki 6-cyfrowe); największa z nich pomnożona przez 2005 daje 108270, a inne wyniki są mniejsze, czyli zaczynają się cyframi 1 i 0, ale wtedy suma cyfr nie przekracza 37,
- dla liczb 7-cyfrowych największa możliwa suma cyfr to 63 i nawet pomnożona przez 2005 nie da liczby siedmiocyfrowej,
- dla większych liczb jest podobnie.
Największa możliwa suma cyfr liczby co najwyżej 5-cyfrowej wynosi 45, zatem w każdym przypadku wystarczy 45 sprawdzeń (od 200X·1 do 200X·45), jednak liczbę tych sprawdzeń można jeszcze zmniejszyć. Ponieważ liczba (L) i suma jej cyfr (S) dają tę samą resztę z dzielenia przez 9, zatem 9|L-S.
a) L - S = 2003S - S = 2002S. Skoro NWD(9, 2002)=1, więc 9|S. Zatem wystarczy 5 sprawdzeń (2003·9, 2003·18, 2003·27, 2003·36 i 2003·45), z czego jedna liczba spełnia warunki zadania: 36054.
b) L - S = 2004S - S = 2003S. Skoro NWD(9, 2003)=1, więc 9|S. Zatem wystarczy 5 sprawdzeń (2004·9, 2004·18, 2004·27, 2004·36 i 2004·45), z czego jedna liczba spełnia warunki zadania: 36072.
c) L - S = 2005S - S = 2004S. Skoro NWD(9, 2004)=3, więc 3|S. Zatem wystarczy 15 sprawdzeń: (2005·3, 2005·6, 2005·9, 2005·12, ..., 2005·45), z czego cztery liczby spełniają warunki zadania: 12030, 24060, 30075, 36090.
Zad. 2. W zadaniu chodziło raczej o konstrukcję teoretyczną, niż możliwość jej fizycznego wykonania.
a) robot ustawi konstrukcję z rysunku.
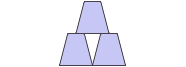
b) Oto jedno z możliwych rozwiązań:
↑ → (2×) ↓ ← (2×) ↑ → (4×) ↓ ← (4×) ↑ → (6×) ↓ ← (6×) ↑ → (8×) ↓ ← (8×) ↑ ↔ → (3×) ↓ ← (3×) ↑ ↔ → (5×) ↓ ← (5×) ↑ ↔ → (7×) ↓ ← (7×) ↑ → (4×) ↓ ← (4×) ↑ → (6×) ↓ ← (6×) ↑ ↔ → (5×) ↓
Zad. 3. Jeśli warunki zadania spełnia więcej niż jedna liczba, należy podać je wszystkie. Oto poprawne odpowiedzi: a) a[tex]\in[/tex](-2/7, -17/64), b) a[tex]\in[/tex](-3/7, -2/5), c) a[tex]\in[/tex]Ø - piłka przelatująca przez kosz nigdy nie zmieści się pod sufitem.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
Strzałki
Jak zapisuje się strzałki?
Strzałki
Można zapisać odpowiedź w dowolnym edytorze i wysłać ją w załączniku do mejla w formacie .pdf. Wprost w treści mejla można używać notacji klawiaturowej -> i <-. Można wreszcie użyć notacji texowej podanej na górnej poziomej belce ("edytor wzorów Texa" klawisz "znaki").