Geometria przestrzenna nie jest szczególnie lubiana przez uczniów. Możecie się jednak przekonać, że nie taki diabeł straszny, jak go malują, rozwiazując przyjemny zestaw zadań 3D. Wystarczy do tego odrobina zdrowego rozsądku, wyobraźni oraz standardowa szkolna wiedza o właściwościach metrycznych prostopadłościanów i ostrosłupów. Stopień trudności rośnie wraz z numerem zadania w zestawie. Początkowe mogą rozwiązać nawet uczniowie z podstawówki. Końcowe wymagają wiedzy licealnej.
Do boju z geometrią 3D
1 komentarz
Czytaj dalej
Szprychy w cylindrze (2) - f-stożki i anty-f-stożki
Czy f-stożki i w-stążki mają coś wspólnego ze sobą nawzajem? Co to w ogóle jest? Jak z f-stożków i anty-f-stożków powstają f-bryły i anty-f-bryły? Zobacz koniecznie! Wcześniej jednak zajrzyj tekstu Szprychy w cylindrze (1) - f-schody.
Szprychy w cylindrze (1) - f-schody
Zaczepiając ruchomy, obrotowy patyk prostopadle do osi i przesuwając płynnie punkt zaczepienia wzdłuż tej osi to w górę, to w dół a jednocześnie obracając patyk wokół osi, wymiatamy nim pewną powierzchnię przypominającą kręte schody. Zobaczmy, jak to wygląda i przyjrzyjmy się powstającym figurom dokładniej.
Ostrosłup do sześcianu
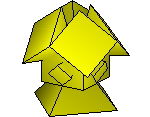Bryła obok jest złączeniem sześcianu i wielu ostrosłupów prawidłowych o dowolnych podstawach, których wierzchołkiem (nieleżącym na podstawie) jest geometryczny środek sześcianu. Spróbujcie przeanalizować podobne, nieco prostsze konfiguracje.
Trzy Korony (2)
Trzy Korony to szczyt Pieninach. Wygląda tajemniczo i pięknie. A jak mógłby wyglądać (widziany oczyma matematyka), gdyby miał Cztery Korony? Zobacz. Najpierw jednak zajrzyj do tekstu Trzy Korony (1). Tam wszystkie korony miały wspólną podstawę, tym razem podstawy mogą mieć różne.
