Autor: Marek Kordos
emerytowany profesor Uniwersytetu Warszawskiego, redaktor naczelny miesięcznika Delta
Proponuję zestaw sześciu zadań, które - moim zdaniem - mogłyby stanowić zestaw maturalny powszechnej matury z matematyki poziomu podstawowego. Sądzę, że zestaw jest kompletny w tym sensie, że ten, kto to go rozwiąże, nie przyniesie ujmy polskiej szkole - rzecz jasna nie jako matematyk, ale jako człowiek kulturalny. Przypuszczam, że nauczyć na tym poziomie można każdego, chyba że wejdzie się z nim w konflikt, nim zacznie się go uczyć. Oczekuję krytyki, ale bardziej zależy mi na konkurencyjnych zestawach zadań. Wierzę, że zbiorową mądrością zdołamy zrobić tę rzecz nie do zrobienia.
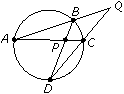 Zadanie 1. Na rysunku [tex] \angle APD = 2 \angle AQD = 60^\circ[/tex]. Obliczyć rozwartości kątów ABD, ACD, BAC, BDC.
Zadanie 1. Na rysunku [tex] \angle APD = 2 \angle AQD = 60^\circ[/tex]. Obliczyć rozwartości kątów ABD, ACD, BAC, BDC.
Zadanie 2. Podać maksymalny zbiór określoności i, dla niego, zbiór wartości funkcji [tex] x+1{/}x [/tex]. Naszkicować jej wykres.
Zadanie 3. W zbiorze [tex] \{49a+35b:a,b\in \mbox{Z}\}\cap\left(\mbox{R}^+\setminus\{0\}\right) [/tex] wskazać liczbę najmniejszą i liczbę najbliższą liczbie 111.
Zadanie 4. Pole powierzchni całkowitej ostrosłupa czworokątnego prawidłowego jest równe 4, a objętość [tex] \sqrt{2}{/}3 [/tex]. Znaleźć długość krawędzi podstawy i wysokości ostrosłupa.
Zadanie 5. Jakie jest prawdopodobieństwo tego, że po losowym pomalowaniu trzech wierzchołków sześcianu na czarno, a pozostałych na biało, żadna ze ścian nie będzie miała wszystkich wierzchołków tego samego koloru?
Zadanie 6. Samolot przy bezwietrznej pogodzie leci z Dęblina do Modlina (d = 120 km) i z powrotem przez godzinę. Ile czasu będzie leciał na tej samej trasie, gdy z Dęblina do Modlina będzie przez cały czas wiał wiatr o prędkości w = 60 km/godz? Zakładamy, że prędkość samolotu względem powietrza jest stała.
Ile punktów przyznać konkretnemu zadaniu to sprawa dyskusyjna. Nie jest jednak (chyba?) dyskusyjny ich podział.
Zadanie 1 Z twierdzenia o kątach wpisanych opartych na tym samym łuku mamy:
Z twierdzenia o kątach wpisanych opartych na tym samym łuku mamy:
[tex] \normalsize \angle ABD = \angle ACD =: \alpha, \;\; \angle BAC = \angle BDC =: \beta [/tex].
Za odkrycie tego przyznajemy 1/3 punktów za zadanie.
Z twierdzenia o kącie zewnętrznym w trójkątach ABP i AQC mamy:
[tex] \alpha + \beta = 60^\circ,\;\; \beta + 30^\circ = \alpha [/tex].
Za odkrycie tego kolejne 1/3 punktów za zadanie.
Stąd (np. dodając stronami) otrzymujemy [tex] \beta = 15^\circ [/tex] i [tex] \alpha = 45^\circ [/tex]. Zadanie 2 Zbiór wartości odnajdujemy np. rozwiązując równanie: [tex] x+1{/}x = a [/tex], czyli [tex] x^2-ax+1=0 [/tex], Wykres należy zaliczyć, gdy będzie w kącie ostrym wierzchołkowym o ramionach Zadanie 3
Za to kolejne 1/3 punktów.
Dziedzina to [tex] R\setminus\{0\} [/tex].
Za to 1/3 punktów za zadanie.
co ma rozwiązanie [tex] (\Delta\geq 0) [/tex] dla [tex] a^2\geq 4 [/tex], czyli [tex] a \in(-\infty, -2] \cup [2, \infty) [/tex].
Za to kolejne 1/3 punktów.
x=0 i x=y.
Za to ostatnie 1/3 punktów.
Ponieważ 49 i 35 dzielą się przez 7, więc wszystkie liczby rozpatrywanego zbioru też dzielą się przez 7.
Za to 1/3 punktów za zadanie.
Dalej 7 = 49 · (-2) + 35 · 3. Można to zgadnąć, sprawdzić przez przejrzenie małych a i b, wreszcie uzyskać z algorytmu Euklidesa:
49 = 35 + 14, 35 = 2 · 14 + 7, skąd 7 = 35 - 2 · 14 = 35 - 2 · (49 - 35).
Stąd pierwsza odpowiedź jest 7.
W każdym przypadku za to kolejne 1/3 punktów.
Pozostaje znalezienie najbliższych 111 wielokrotności 7.
111 : 7 = 15 r. 6, skąd mamy, że druga odpowiedź to 7 · 16 = 112.
Znów 1/3 punktów.
Za obliczenie konkretnych wartości dla a i b w tym przypadku - 0 punktów, bo nikt o to nie pyta.
Zadanie 4
Gdy oznaczymy bok przez [tex] a [/tex], a wysokość przez [tex] h [/tex], wysokość ściany bocznej będzie równa [tex] \sqrt{h^2+(a/2)^2} [/tex], zatem do rozwiązania jest układ równań:
[tex] a^2+4\cdot \frac{a}{2} \cdot \sqrt{h^2+(a/2)^2}= 4 [/tex], [tex]\ \ \frac{1}{3}a^2h= \frac{\sqrt{2}}{3} [/tex] .
Za to 1/3 punktów za zadanie.
Dalej [tex] a^2 + a\sqrt{4h^2+a^2}= 4 [/tex] , [tex] a^2h=\sqrt{2} [/tex] , co po podstawieniu [tex] h =\sqrt{2}{/}a^2 [/tex] daje:
[tex] a^2+a\sqrt{8/a^4+a^2} = 4 [/tex], czyli [tex] \sqrt{8/a^4+a^2} = 4-a^2 [/tex].
Po podniesieniu do kwadratu mamy: [tex] 8{/}a^2 + a^4 = 16 - 8a^2 + a^4 [/tex] ,
co po pomnożeniu przez [tex] a^2{/}8 [/tex] daje: [tex] a^4 - 2a^2 + 1 = 0 [/tex], a zatem [tex] (a^2 - 1)^2 = 0 [/tex], czyli [tex] a^2=1 [/tex].
Mamy więc [tex] a=1 [/tex] i [tex] h=\sqrt{2} [/tex].
Za te rachunki 2/3 punktów przyznanych dla tego zadania.
Zadanie 5
Ponieważ każdy wierzchołek należy do trzech ścian, więc średnia liczba białych wierzchołków na ścianie to [tex] \frac{3\cdot 5}{6} > 2 [/tex]. Zatem istnieje (co najmniej jedna) ściana, na której są (co najmniej) 3 wierzchołki białe. Zawsze możemy tak postawić sześcian, że będą to wierzchołki A, B, C ściany dolnej.
Za takie zredukowanie problemu 2/3 punktów za zadanie.
Pozostałe dwa białe wierzchołki mogą być wylosowane spośród pozostałych pięciu, a więc na [tex] {{5}\choose{2}} = 10 [/tex] sposobów. Nazwijmy brak ściany o czterech białych wierzchołkach sukcesem. Jeśli ma być sukces, nie może zostać wylosowany czwarty wierzchołek D ściany dolnej i pozostałe dwa białe wierzchołki muszą się znaleźć na górnej ścianie. Spośród możliwych sześciu par sukces zapewniają cztery: wszystkie trzy z D' oraz (A', C'). Zatem poszukiwane prawdopodobieństwo to 0,4.
Za to pozostałe 1/3 punktów.
Zadanie 6
Prędkość samolotu względem powietrza to 2d, zatem przy wietrze o prędkości
w będzie on leciał przez
d/(2d + w) + d/(2d - w) = d/(4d2 - w2) · (2d - w + 2d + w) = 4d2/(4d2 - w2) =
= 1 + w2/(4d2 - w2).
Podczas gdy rozwiązanie bez użycia ogólnych symboli to:
do Modlina z prędkością 240 + 60 = 300 km/godz przez 2/5 godz, czyli 24 min,
z Modlina do Dęblina z prędkością 240 - 60 = 180 km/godz przez 2/3 godz, czyli 40 min. Łącznie daje to czas o 4 minuty gorszy, niż bez wiatru.
Za rozwiązanie tylko liczbowe 2/3 punktów za zadanie, za rozwiązanie symboliczne 1/3 punktów, za poprawny wynik w obu przypadkach dalsze 1/3 punktów.




 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

Uwaga do rozwiązania zad. 5
Pomysł "zamiast teoretycznej dyskusji" jest świetny. Tymczasem jednak mam konkurencyjne rozwiązanie zadania 5.
Jeśli jest 'źle', to jakaś ściana ma wszystkie wierzchołki białe. Wtedy czarne są trzy wierzchołki na przeciwległej ścianie. Czyli jest źle, gdy czarne leżą na jednej ścianie, którą wybieramy na 6 sposobów i na każdej z nich na 4 sposoby malujemy jej trzy wierzchołki na czarno.
Stąd jest źle z prawdopodobieństwem $\frac{6\cdot 4}{{8}\choose{3}} = 3/7$. Więc prawdopodobieństwo, o które pytają w zadaniu to 4/7.
To jest na pewno bardziej standardowe rozwiązanie, zakłada bowiem, że wszystkie wybory kolorowanych wierzchołków są jednakowo prawdopodobne.
No właśnie!
Właśnie temat: "jak uniezależnić (i kiedy się da) wynik zadania probabilistycznego od wyboru 'maszyny losującej' albo "czy uznawać za jednakowo poprawne rozwiazania takich zadań, gdy wybór maszyny losującej powoduje róznicę uzyskanych wyników" albo... wydaje mi się jednym z oczekiwanych nurtów dyskusji na tym forum.
Oba są OK
Oczywiście oba rozwiązania są poprawne i oba należałoby uczniom uznać. Trzeba im tylko wytłumaczyć, skąd się wzięła różnica. To jest tak, jak np. w paradoksie Bertranda.
A co z tzw. ekspertami?
Wytłumaczenie tego uczniom, to tzw. małe piwo. Ale co z "ekspertami" z CKE? Tu wietrzę prawdziwe kłopoty.