Zad. 1. Oblicz
|
4 x 4 |
7 x 7 67 x 67 667 x 667 6667 x 6667 .................... |
Opisz i wyjaśnij zauważone prawidłowości. Czy zachodzą one także dla innych cyfr początkowych? Jeśli nie, to dlaczego?
Zad. 2. Oblicz na kalkulatorze prostym, używając jak najmniej klawiszy:
a) silnię 10,
b) sumę silni pierwszych 10 liczb naturalnych,
c) sumę odwrotności silni pierwszych 10 liczb naturalnych,
d) sumę silni odwrotności pierwszych 10 liczb naturalnych.
Przyjmujemy, że liczby naturalne zaczynają się od 1.
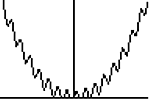
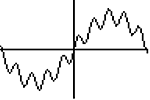
Zad. 3. Jaki wzór funkcji da na ekranie komputera lub kalkulatora graficznego efekt tzw. paraboli Parkinsona (paraboli rysowanej jakby trzęsącą się ręką, patrz szkic obok), a jaki - sinusoidy Parkinsona?
Nikt nie uzyskał w tym miesiącu maksymalnej liczby punktów. Po 2,5 pkt. zdobyli: Kamila Bojar z ZSP w Szprotawie, Andrzej Piasecki - administrator IT z Oleśnicy i Marzena Wąsiewicz - informatyk, a obecnie gospodyni domowa z Kajetan, po 2 pkt.: Krystyna Lisiowska -
redaktor z Warszawy i Krzysztof Danielak z I LO w Jeleniej Górze, po 1,5 pkt. - Tomasz Skalski - student matematyki na Politechnice Wrocławskiej i Wojciech Tomiczek - inżynier z Lipowej. Pozostali zawodnicy uzyskali poniżej 1 pkt.
W czołówce Ligi kalkulatorowo-komputerowej (z punktami na 24 możliwe) znajdują się:
- Marzena Wąsiewicz (21,5 pkt)
- Krystyna Lisiowska (20 pkt)
- Andrzej Piasecki (19 pkt)
- Daria Bumażnik z II LO w Jeleniej Górze i Tomasz Skalski (16,5 pkt).
Zad. 1.
|
4 x 4 = 16 |
7 x 7 = 49 67 x 67 = 4489 667 x 667 = 444889 6667 x 6667 = 44448889 .................... |
W tych przykładach każdy następny wynik powstaje z poprzedniego przez wstawienie "w środek" liczby o 1 mniejszej niż pierwszy wynik. Prawidłowość ta powtarza się dla wszystkich dalszych liczb w każdej z kolumn.
Własność tę można łatwo uzasadnić. Zachodzi np.:
334 × 334 = (300+34) × (300+34) = 90000 + 6·34·100 + 34×34 =
90000
1156
+ 20400
________
111556
W kolejnych wierszach ta sama sytuacja występuje w wyższych rzędach dziesiętnych, np.:
33334 × 33334 = (30000+3334)×(30000+3334) = 900000000 + 6·3334·10000 + 3334×3334 =
900000000
11115556
+ 200040000
___________
1111155556
Analogicznie:
667 × 667 = (600+67) × (600+67) = 360000 + 12·67·100 + 67×67 =
360000
4489
+ 80400
________
444889
66667 × 66667 = (60000+6667)×(60000+6667) = 3600000000 + 12·6667·10000 + 6667×6667 =
3600000000
44448889
+ 800040000
_____________
4444488889
Ogólna procedura "weź liczbę jednocyfrową i pomnóż przez siebie, a w następnym kroku dopisz przed każdym z czynników cyfrę o 1 mniejszą niż w pierwszym czynniku" nie zachowuje prawidłowości zaobserwowanych dla powyższych przykładów w żadnym innym przypadku.
Tymczasem można zaobserwować inne prawidłowości, np.
|
2 x 2 = 4 |
9 x 9 = 81 89 x 89 = 7921 880 x 889 = 790321 8889 x 8889 = 79014321 88889 × 88889 = 7901254321 888889 × 888889 = 790123654321 .................... |
Tym razem każdy następny wynik powstaje z poprzedniego przez wstawienie "w środek" liczby o 11 większej niż wstawiana w poprzednim kroku (liczbę 4 traktujemy jako 04), a dokładniej liczby, w której zarówno cyfra dziesiątek jak i jedności rośnie o 1 w stosunku do poprzednio wstawianej liczby, przy czym po 9 jest w tym ciągu 0.
Czy możliwe są jeszcze inne prawidłowości w analogicznych eksperymentach numerycznych dla innych cyfr?
Zad. 2.
a) 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 =
19 klawiszy
b) MC 1 M+ × 2 M+ × 3 M+ × 4 M+ × 5 M+ × 6 M+ × 7 M+ × 8 M+ × 9 M+ × 10 M+ MR
32 klawisze, można jeszcze opuścić znak mnożenia przed cyfrą 2
c) MC 1 M+ : 2 M+ : 3 M+ : 4 M+ : 5 M+ : 6 M+ : 7 M+ : 8 M+ : 9 M+ : 10 M+ MR
32 klawisze
d) Istnieje co prawda uogólnienie pojęcia silnii dla dowolnych liczb rzeczywistych (zwane funkcją gamma Eulera), ale sama silnia zdefiniowana jest tylko dla liczb naturalnych i zera, zatem działanie podane w zadaniu jest niezdefiniowane.
Zad. 3. Parabola np. x2+2sin(10x), zakres ekranu -5<x<5, 0<y<25. Sinusoida np. sinx+0.25sin10x, zakres ekranu -3<x<3, -1,5<y<1,5.
 |
 |
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
