Zadanie 1. W trójkącie ABC kąt B ma 120°. Niech X, Y, Z oznaczają spodki dwusiecznych odpowiednio kątów A, B i C. Oblicz miarę kąta XYZ.
Zadanie 2. Na bokach AC i BC trójkąta ostrokątnego zbudowano prostokąty BERS i AFMN, gdzie E jest spodkiem wysokości opuszczonej z wierzchołka A, a F spodkiem wysokości opuszczonej z wierzchołka B. Ponadto ER = BC i FM = AC. Wykaż, że pole kwadratu zbudowanego na AB równe jest sumie pól danych prostokątów.
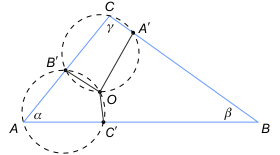
Zadanie 3. Wykaż, że jeśli na bokach BC, AC i AB trójkąta wybrać odpowiednio punkty A', B' i C' różne od wierzchołków, to okręgi opisane na trójkątach AB'C', BA'C' i CA'B' mają punkt wspólny.
W czerwcowej serii komplet punktów zdobył jedynie pan Krzysztof Sobków - nauczyciel II LO w Opolu.
Najwyższe wyniki w Lidze z Geometrii Elementarnej w roku 2013/14 uzyskali (w nawiasie podajemy liczbę uzyskanych punktów na 270 możliwych):
- Krzysztof Sobków - nauczyciel II LO Opole (260 pkt)
- Jacek Bagiński - nauczyciel I LO Kraków (256 pkt)
- Arkadiusz Wróbel - student Brwinów (248 pkt)
- ex aequo Daria Bumażnik - uczennica II LO Jelenia Góra i Tadeusz Porzucek - emeryt Gostyń (194 pkt)
- ex aequo Włodzimierz Bąk - nauczyciel I LO Opole i Anna Gudełajtis - uczennica II LO Opole (170 pkt)
- Michał Demski - nauczyciel SP Smolec (110 pkt)
- Katarzyna Kozińska - nauczycielka SP Leonardo da Vinci Wrocław (98 pkt)
- ex aequo Maciej Cebula - uczeń I LO Olesno i Antoni Kamiński uczeń III LO Wrocław (82 pkt)
Wszystkim serdecznie gratulujemy!
Zadanie 1
Obierzmy punkt K na prostej AB jak na rysunku. Zauważmy, że BC jest dwusieczną kąta KBY, zatem X jest środkiem okręgu dopisanego do trójkąta ABY. Oznacza to, że YX jest dwusieczną kąta BYC, a stąd kąt XYZ jest prosty jako kąt między dwusiecznymi kątów przyległych (BYC i BYA).
Zadanie 2
Niech P1 i P2 oznaczają pola prostokątów zbudowanych na bokach trójkąta (jak na rysunku). Zauważmy, że na czworokącie ABEF można opisać okrąg (bo kąty AFB i AEB są proste). Zatem z twierdzenia o siecznych okręgu (tzw. potęga punktu względem okręgu) mamy CE·CB = CF·CA lub równoważnie (CB-BE)CB = (CA-AF)CA, co daje CB2 - P1 = CA2 - P2 (♥). Z kolei z twierdzenia Pitagorasa mamy AB2 = AE2 + BE2 = AC2 - CE2 + BE2 = AC2 - (BC-EB)2 + BE2 = AC2 - BC2 + 2BC·EB = AC2 - BC2 + 2P1 = P1 + P2 (na mocy ♥).
Zadanie 3
Niech O będzie puktem wspólnym dwóch okręgów jak na rysunku. Wystarczy wykazać, że kąt A′OC′ sumuje się z kątem β do 180° (wtedy na czworokącie BA'OC' można opisać okrąg), czyli że jest równy α+γ. Jest tak, bowiem kąt B'OA′ = 180° - γ (z warunku wpisania czworokąta w okrąg), a kąt B'OC′ = 180° - α. Kąt A'OC' sumuje się z poprzednimi do 360°, więc ma miarę α+γ.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
