|
W wielu podręcznikach rzut ukośny jest omawiany z użyciem
trygonometrii i pochodnych. Okazuje się, że gdy 'zaufamy wektorom', nie trzeba aż tak zaawansowanej wiedzy z matematyki. Wystarczy znać twierdzenie Pitagorasa (i trochę fizyki!).
Problem
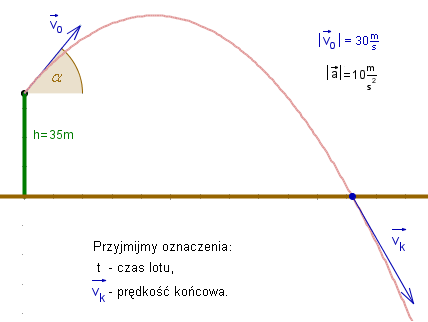
Rzut ciała o masie m = 0,1 kg, z szybkością v0 = 30 m/s,
pod kątem 
, z wysokości h = 35 m.
Dla jakiego
zasięg jest największy?
Zacznijmy od tego, że nie wieje wiatr i pomijamy opory powietrza.
Zatem na ciało działa jedynie STAŁA siła przyciągania skierowana pionowo w dół.
Siła ta (jak mówi Newton) zmienia prędkość ciała.
Zmiana prędkości w jednostce czasu to przyśpieszenie, precyzyjniej:
różnica prędkości podzielona przez czas, to jest średnie przyśpieszenie (ważne, że tu chodzi o wektory!):
Ponieważ siła jest STAŁA, to przyśpieszenie jest STAŁE, skierowane w dół, równe g=10 m/s2.
Równość ta jest pokazana na rysunku (zaczepiamy wektory prędkości w jednym punkcie).
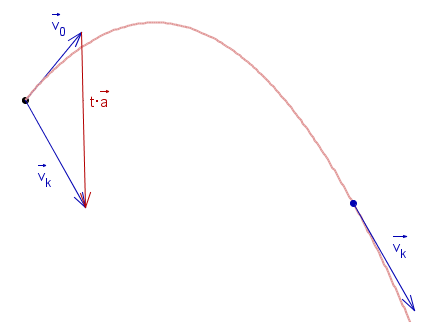
Uwaga. Fizycy ten 'trójkąt' przeczytają tak (mnożąc boki przez m): popęd jest równy zmianie pędu.
Teraz najważniejsze:
szybkość przy lądowaniu (wielkość
)
jest stała, tj. nie zależy od kąta
.
Mianowicie energia na początku i na końcu lotu jest taka sama: E0 = Ek, czyli
Zaznaczmy na rysunku okręgi o promieniach równych
i
, to na nich leżą końce pionowego odcinka, niezależnie od kąta
.
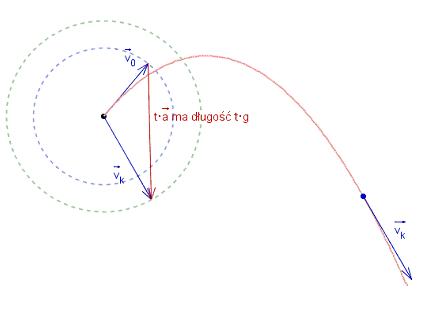
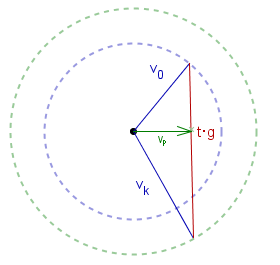
Dorysujmy 'poziomą' wysokość tego trójkąta (prostopadłą do pionowego boku).
Ma ona długość vp składowej poziomej wektora
.
Pole tego trójkąta jest równe
. vp . t g = (vp.t ) .
(g) ,
g)
.
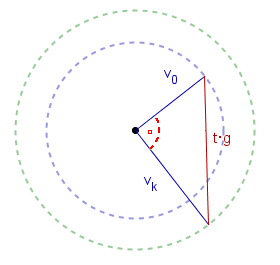
Zatem
a pole jest największe, gdy boki są prostopadłe.
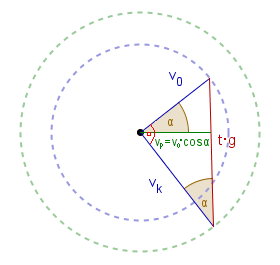
Z takiego trójkąta prostokątnego można niemal wszystko odczytać.
Mianowicie w locie o maksymalnym zasięgu:
- kąt, pod którym ciało będzie wbijać się w ziemię, jest równy
90o - ,
- zasięg jest równy polu trójkąta podzielonemu przez g,
czyli
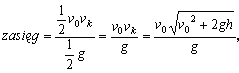
- lot trwa (z tw. Pitagorasa wyznaczamy przeciwprostokątną, skąd znajdujemy czas t)
-
zasięg maksymalny otrzymamy przy rzucie pod kątem
, którego tangens jest równy
skąd
37o.
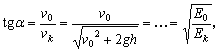
Uwaga. Tak rozwiązywane zadania można znaleźć w świetnej książce 'Matematyka w szkole średniej', tomy 1-3, WSiP, Warszawa 1988 (jest to polski przekład brytyjskiego podręcznika do matematyki wydanego przez Cambridge University Press).
