Łatwo jest opanować wzory na pochodne funkcji elementarnych i reguły obliczania pochodnych funkcji złożonych. Zadania dotyczące wykresów funkcji i ich pochodnych pozwalają sprawdzić, na ile uczeń rozumie te pojęcia i zależności między nimi. Proponujemy kilka zadań rachunkowych na ten temat.
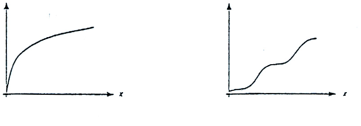
Zad. 1a. Oto wykres pewnej funkcji. Naszkicuj w tym samym układzie współrzędnych jej pochodną.
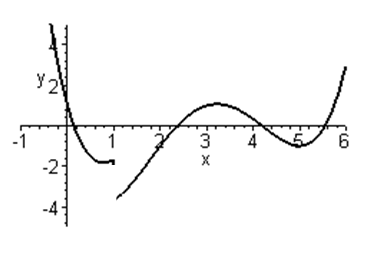
Zad. 1b. Oto wykres pochodnej pewnej funkcji. Naszkicuj w tym samym układzie współrzędnych tę funkcję.
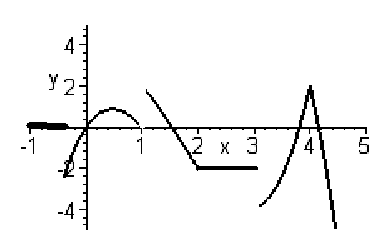
Zad. 2. Uporządkuj następujące funkcje (pokazane na diagramie) zgodnie z szybkością wzrostu w punkcie x = 0. Jak łatwo poznać, która z nich jest która?
a) x, b) sinx, c) tgx, d) ln(x–1), e) x2, f) 2x–1

Zad. 3a. Dane są wykresy funkcji f i g i jeszcze kilka innych wykresów w przypadkowej kolejności. Uporządkuj je w ciąg, w którym następny wykres przedstawia pochodną poprzedniej funkcji.
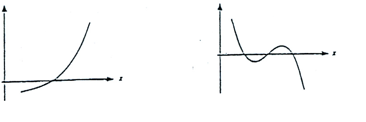 g(x)
g(x)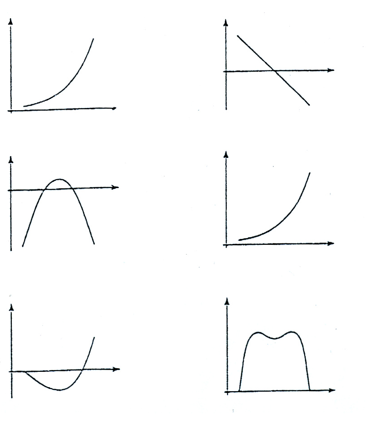
Zad. 3b. Dane są wykresy funkcji f i g i jeszcze
kilka innych wykresów w przypadkowej kolejności. Uporządkuj je w ciąg, w którym następny wykres przedstawia pochodną poprzedniej funkcji.
 g(x)
g(x)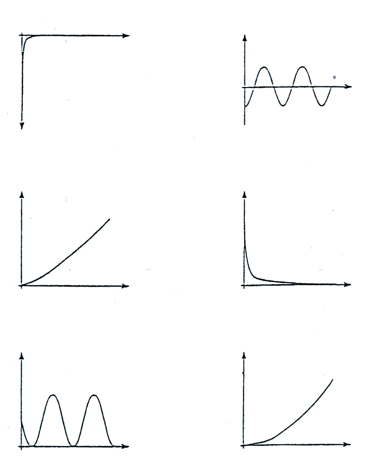
Wymyśl kolejne zadania wykorzystujące wykresy funkcji i ich pochodnych.







